電子線回折

実験番号:UE5010500
箔状の多結晶グラファイトによる電子線回折の実験から,電子が波の性質を持つことの証拠が得られます。電子線回折管の蛍光スクリーン上に電子線の軸上の中心スポットを囲む2つの回折環が観察できます。これらの回折環は,グラファイト箔内にある微結晶中の,ブラッグの反射条件を満たす格子面で生じた,電子線回折に起因します。この現象は,結晶性粉末による,X線のデバイ-シェラー回折で得られる結果に類似しています。
実験の手順
- 異なる加速電圧に対して,2つの回折環の直径を測定します。
- 異なる加速電圧に対して,ブラッグの反射条件を適用し,電子線の波長を求めます。
- 得られた電子の波長に対して,ド=ブロイの関係式が成り立つことを確かめます。
実験に必要な機器
- U185711:電子線回折実験管・S型 ×1
- U185002:陰極線管ホルダー・S型 ×1
- U138021:プラグ付き安全リード線・75cm・15本セット ×1
- 5kV高圧直流電源装置 ×1 (別途ご用意ください)
- 直流電源(10V/3A) ×1 (別途ご用意ください)
実験解説書
英語版 実験手順書 ダウンロード(参考,一部取り扱いのない製品も含まれています)
基本原理
ルイ・ド=ブロイは1924年に,粒子が原理的に,波としての性質も持つという仮説を押し進めて, その波長が運動量に依存するという仮説を提案しました。彼の理論は後に,C.ディヴィソンとL.ジャー マーによって,結晶質のニッケルによる電子線の回折現象を観察することにより,確かめられました。
ド=ブロイによると,粒子の波長λと運動量p との間には,以下のような関係が成り立ちます:
(1)
ここで,h はプランク定数を表します。
電圧UAで加速された電子の場合,これは以下のような式になります。
(2)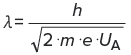
ここで,mは電子の質量を,e は素電荷を表します。
例えば,加速電圧が4kVの場合,電子の波長は約20pmになります。
本実験で電子の波動性は,真空にしたガラス管の中に置いた多結晶グラファイトからの,電子線の回折現象を観察することによって示されます。電子線回折管の蛍光スクリーン上には,電子線の軸上に生じる中心スポットを囲む回折環が観察されます。回折環の直径は,加速電圧に依存します。これらの回折環は,微結晶中にある,下記のブラッグの反射条件を満たす格子面で生じた,電子線回折に起因します:
(3)![]()
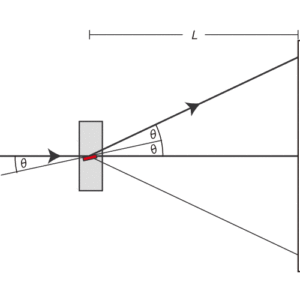
ここで,θはブラッグ角,n は回折次数,d は格子面間隔を指します。ブラッグ角がθの時の回折環の直径は,以下の式で与えられます(図2を参照):
(4)![]()
ここでL は,グラファイト箔と蛍光スクリーン間の距離を指します。
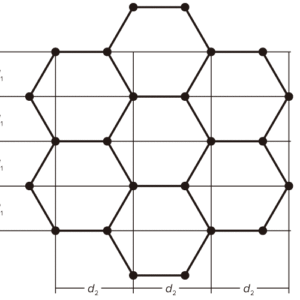
グラファイトの結晶構造には,2つの異なる格子面間隔d1= 123pmとd2= 213pmがあるので(図3を参照),一次(n= 1)の回折パターンは,直径D1とD2の2つの回折環から成ります。評価
2つの回折環の直径と格子面間隔を使って,ブラッグの反射条件を適用することにより,波長λを求めることができます。回折角が小さい場合には,式(3)と(4)から,以下の方程式が成り立ちます:
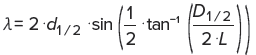
こうして得られる波長の実験値は,理論式( )から計算される値と比較できます。
参考資料
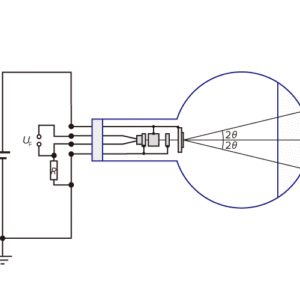
-
図1:電子線回折管の概略図。
-
図2:グラファイト箔中の典型的な微結晶内にある,本実験に好適な角度を有する結晶面の一群からのブラッグ反射。
-
図3:グラファイトの結晶構造。
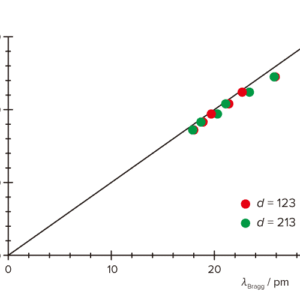
-
図4:ブラッグの反射条件を使って実験的に求められる波長と,ド=ブロイの理論による波長との関係。