平板コンデンサーのつくる静電場

実験番号：UE3010800

帯電した平板コンデンサの電極間距離が短い場合は一様な静電場が発生します。これを電荷が逃げないようにして電極間距離と電圧を測定することで確認します。

また，誘電体を間に挟んだときの電圧変化から比誘電率を求め，誘電体の働きを考えます

実験の手順

• 帯電した平板コンデンサーの電極間距離を変化させ，その時の電極間電圧を測定します。
• 電極間距離が小さい時に，電圧と電極間距離が比例することを確かめます。
• 誘電体を電極間に挟んだときの電圧から比誘電率を求めます。

実験に必要な機器

• U8557820-115：電場計 ×1
• U8492355：可変平板コンデンサー・D型 ×1
• U8492341：フェノール樹脂積層板 ×1
• U8476371：アクリル製誘電板 ×1
• U13801：低電圧用リード線・75cm・15本セット ×1
• U8557330：アナログマルチメーター ESCOLA30 ×1

お見積りフォーム

実験解説書

実験解説書 ダウンロード（PDF）

英語版 実験手順書 ダウンロード（参考，一部取り扱いのない製品も含まれています）

基本原理

帯電した平板コンデンサの電極間には引力が働いています。その為，電極間距離を広げるには，力学的な仕事が必要となります。この仕事によるエネルギーの増加は電極間の電圧が増加することで確かめられます。電極の移動距離と電圧が比例関係にあれば，その時の電場は一様であると言えます。

また電極間距離を保ったまま誘電体を間に入れると，電圧変化が生じます。この時の電圧変化から誘電体の比誘電率を計算することができます。

本実験では電圧測定時に平板コンデンサーに蓄えられた電荷が逃げないようにすることが重要です。その為，電圧は電場計を用いて静電圧を測定します。

i)，電極間静電場の一様性

平板コンデンサーの電場をガウスの法則を使って計算することで，平板電極間の静電場が一様である事が示されます。それは電極間面積が十分大きい（電極端部を考えない）という条件での結果です。

式で表わせば

(1)\( E = \frac { 1 } { \varepsilon_0 } \cdot \frac { Q } { A } \)

ε0は真空の誘電率：\( \varepsilon_0 = 8.85 \times 10^{-12} \left[ \frac { F } { m } \right] \)A：平板コンデンサー電極面積

電位の定義から，電場を積分したものが電位なので電場が一様であれば電極間距離dと電位差（＝電圧）Uは比例し，次の関係になります。

(2)\( U = E \cdot d \)

この関係を実験で検証します。

ii)，誘電体の比誘電率

誘電体（絶縁体）は電流を流しませんが，これを平板コンデンサー電極間に挿入すると電圧変化が起こります。この時の電圧を間に何も挟まない時の式(1)と(2)と同様の関係式で書けるとし，次のようにします。

(3)\( U’ = E’ \cdot d \\ E’ = \frac { 1 } { \varepsilon_r \cdot \varepsilon_0 } \cdot \frac { Q } { A } \\ \therefore \,\, U’ = \frac { 1 } { \varepsilon_r \cdot \varepsilon_0 } \cdot \frac { Q } { A } \cdot d = \frac { 1 } { \varepsilon_r } \cdot U \\ \frac { U } { U’ } = \varepsilon_r \)

この時のε_rを比誘電率といいます。式（3）から分かるように，サンプルの誘電率と真空の誘電率の比に当たります。

(4)\( \therefore \, \, U’ = \frac { 1 } { \varepsilon_r \cdot \varepsilon_0 } \cdot \frac { Q } { A } \cdot d =\frac { 1 } { \varepsilon_r } \cdot U \\ \frac { U } { U’ } = \varepsilon_r \)

評価

i)，電極間静電場の一様性

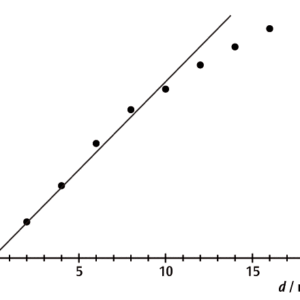
実験で測定された電極間距離と電圧をグラフにすると，電極間距離dが大きくなると比例関係を表す直線上から外れてきます。（図1） これは，その電極間隔では電場Eが一様という仮定が成り立たなくなるためです。

ii)，誘電体の比誘電率

• 実測し，下記の値を得ました。
• 電極間に何も挟まない状態での電圧U=10 V
• フェノール樹脂積層板を挟んだ場合の電圧U1=2.2 V
• アクリル板を挟んだ場合の電圧U2=2.9 V

これらのデータより比誘電率εrはそれぞれ

$$ \varepsilon_{ r1 } = \frac { 10\,\,V } { 2.2\,\,V } = 4.5 \\ \varepsilon_{ r2 } = \frac {10\,\,V } { 2.9\,\,V } =3.4 $$

となります。実験から得られた比誘電率は文献値と良い一致を示しています。

• 参考：比誘電率
• フェノール樹脂積層板：4.6～5.5
• アクリル板：2.7～4.5

この誘電体の働きは誘電分極によるものです。また，この性質により誘電体をコンデンサー間に挟むことにより同じ電圧を印加した場合，より大きな電荷を蓄えることができます。（比誘電率がεr＞1のため。）

$$U = \frac { d } { \varepsilon_{ r } \cdot \varepsilon_{ 0 } \cdot A } \cdot Q \\ \therefore \,\, Q = \frac { \varepsilon_{ r } \cdot \varepsilon_{ 0 } \cdot A } { d } \cdot U \equiv C \cdot U$$

このCを静電容量と言います。これより，電極間距離dと電極面積Aが等しい平行板コンデンサーに同じ電圧Uを印加した場合でも，コンデンサーが蓄える電荷量の比は比誘電率の比となります。

$$ U = \frac { Q_1 } { C_1 } = \frac { Q_2 } { C_2 } \\ \frac { Q_1 } { Q_2 } = \frac { C_1 } { C_2 } = \frac { \frac { \varepsilon_{ r1 } \cdot \varepsilon_{ 0 } \cdot A } { d } } { \frac { \varepsilon_{ r2 } \cdot \varepsilon_{ 0 } \cdot A } { d } } = \frac { \varepsilon_{ r1 } } { \varepsilon_{ r2 } } $$

実際に使用されるコンデンサーは誘電体を使って，静電容量を大きくしています。

参考資料