メートルブリッジ回路

実験番号:UE3020300
電位の等しい部分間では電荷の移動が起こらないため,電流が流れません。この事を使い,抵抗値を精密に測定する手法の一つがホイートストンブリッジ回路です。 一般的な電流計は微小でも内部抵抗があり,抵抗値を測定する際に内部抵抗値による誤差が問題となる場合があります。 一方,ホイートストンブリッジでは電流が流れない平衡状態を作り,その時の抵抗比から被測定抵抗の抵抗値を計算します。この手法の利点は電流が流れないことから,余分な電圧降下が無視できることや,電源,検流計,回路を流れる電流値に依存しない測定ができることです。 ここでは可変抵抗部分を抵抗線分割に置き換えたメートルブリッジ回路で測定します。
実験の手順
- 被測定抵抗と精密抵抗器,抵抗ブリッジと電源,検流計を回路図のように接続します。
- 電源を入れ,抵抗ブリッジのスライドを動して,検流計の電流値が0になるようにします。
- 抵抗比から被測定抵抗値を計算します。
- 複数の測定値を組み合わせて計算から結果を出す場合の誤差を考え,これを元に計算された抵抗値の精度を評価します。
実験に必要な機器
- U8551002:抵抗ブリッジ ×1
- U11182:10段階可変抵抗・10~100Ω ×1
- U11183:10段階可変抵抗・100~1kΩ ×1
- U11184:10段階可変抵抗・1k~10kΩ ×1
- U51006:抵抗器・100Ω ×1
- U51007:抵抗器・1kΩ ×1
- U138021:プラグ付き安全リード線・75cm・15本セット ×1
- 直流電源(10V/3A) ×1 (別途ご用意ください)
- 検流計 ×1 (別途ご用意ください)
実験解説書
基本原理
電位が等しい部分間では電流が流れないという平衡状態を検出するので,検流計の最小目盛などに依存しないで正確に検出できます。この手法を零位法といいます。この時の回路抵抗比から被測定抵抗の抵抗値を計算で求めます。
実験詳細手順
- 図1の様に回路をセットします。
- 検流計の測定レンジは最大に設定します。
- 抵抗ブリッジのスライダーを真ん中(~50cm)程度に移動します。
- 電源電圧を0から徐々に上げていき,5Vにします。
- その時,検流計の針が振り切れないように,適宜,抵抗ブリッジのスライダーを動かしていきます。
- 検流計の針が0を指したら検流計の測定レンジを切り替えて,最小レンジでも針が0を指すように,測定レンジごとに注意深くスライダーを調節します。
- 検流計が最小レンジで0を指しているときの抵抗ブリッジの目盛(長さ)を0.5mm単位で測定します。
- 時間があれば同一の被測定抵抗に対して数回測定を繰り返して,スライダー位置にズレがないか確認します。
- また,更に余裕があれば電源電圧を2.5V,7.5Vなど変えて,その時の平衡状態になるスライダー位置を測定します。
- 別の被測定抵抗でも同様の測定を繰り返します。
-
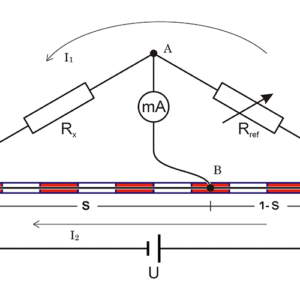
図1:測定回路図 Rx:被測定抵抗,Rref:基準抵抗(ここでは10段階可変抵抗)
検流計に電流が流れていないので,その間の電位は等しくなっています。また,被測定抵抗を含む上側の抵抗2つ(RxとRref)を流れる電流I1は\( I_1=\frac {U} {R_x+R_{ref}} \) となります。同様に抵抗ブリッジを流れる電流I2は\( I_2=\frac {U} {R_{bridge}} \)です。
検流計に電流が流れないことからA,B点の電位は等しくなるため,抵抗ブリッジの抵抗線(NiCr)の抵抗率をρ,断面積をA,スライダーの位置をs(m)とすると,次のように表せます。
\[ V_A=R_x \cdot I_1=R_x \cdot \frac {U} {R_x+R_{ref}} \]
\[ V_B=\rho \cdot \frac{s} {A} \cdot I_2=\rho \cdot \frac {s} {A} \cdot \frac {U} {\rho \cdot \left( \frac {s} {A} + \frac {1-s} {A} \right) } =s \cdot U \]
\[ V_A=V_B \text{より,} R_x \cdot \frac {U} {R_x+R_{ref}} =s \cdot U \]
(1) \[ \therefore R_x=R_{ref} \cdot \frac {s} {1-s} \]
このように電源電圧・回路電流値と関係なく,既知抵抗値の比で被測定抵抗値が計算できます。特にメートルブリッジの場合,抵抗線長の比で表わすことができます。
評価
メートルブリッジ回路の感度
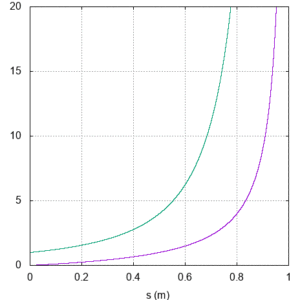
ここでは感度をスライダーの移動に対するRx/Rrefの変化率とします。当然,sが大きくなるほどRx/Rrefは大きくなり,一つのRrefで測定できる被測定抵抗値も大きくなります。 ただし,感度も大きくなるため,抵抗ブリッジのスライダーを手で動かすことから,あまり変化率が大きいと調節が困難となります。よって,図2から見て取れるようにs≦0.7mになるようにRrefを選ぶと調節しやすいでしょう。
-
図2:メートルブリッジの感度 赤:縦軸-Rx/Rref,緑:縦軸-Rx/Rrefの変化率
測定値からの計算による値の誤差
測定誤差が偶然誤差であり,かつ正規分布しているとすると仮定すると,一般に求めたい値fが測定値(a,b,c,,…)の関数である場合,誤差の期待値は次のように書けます。
\[ |\Delta f|=\sqrt { \left( \frac { \partial f }{ \partial a } \cdot \Delta a \right)^2 + \left( \frac { \partial f }{ \partial b } \cdot \Delta b \right)^2 + \left( \frac { \partial f }{ \partial c } \cdot \Delta c \right)^2 + \cdots } \]
この両辺をfで割ると
(2) \[ \left| \frac {\Delta f} {f} \right|= \sqrt { \left( \frac { \partial f }{ \partial a } \right)^2 \cdot \left( \frac {\Delta a} {f} \right)^2 + \left( \frac { \partial f }{ \partial b } \right)^2 \cdot \left( \frac {\Delta b} {f} \right)^2 + \left( \frac { \partial f }{ \partial c } \right)^2 \cdot \left( \frac {\Delta c} {f} \right)^2 + \cdots } \]
となります。
今回の被測定抵抗値計算ではRrefの精度と長さsの読取精度が偶然誤差となっており,よって被測定抵抗値Rxの相対誤差の期待値は
(3) \[ \left| \frac { \Delta R_{ x } }{ R_{ x } } \right| =\sqrt { \left( \frac { \Delta R_{ ref } }{ R_{ ref } } \right)^2 + \left( \frac { \Delta s }{ s } \right)^2 \cdot \left( \frac { 1 }{ 1-s } \right)^2 } \]
と表せます。
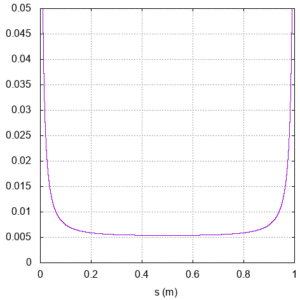
Rrefに使用する抵抗器の公差は±0.5%であり,sの読み取り誤差を±0.5mmとして上記を計算すると図3となります。
-
図3:メートルブリッジの相対誤差(被測定抵抗値に対する誤差割合)
よって本回路で測定する場合,特に高い精度が必要であればs=0.5m近辺となるようなRrefを選ぶ必要があります。求めているのが一般的な精度だとしても0.2m≦s≦0.8mの範囲となるよう注意が必要です。
(3)式を使って被測定抵抗値Rxの誤差(の期待値)まで含めて示すと,前ページの表1のようになります。
スライダー位置sが抵抗ブリッジ中央付近にないときの算出抵抗値は誤差まで含めると,被測定抵抗の公称値±公差を外れています。 しかし,これまで検討してきたメートルブリッジ回路の感度や誤差の大きさからするとs=50cm近辺の値が最も確からしいと考えられ,その場合,誤差まで含めても公称値±公差の範囲に測定値が入っています。
抵抗ブリッジの抵抗線長(L=1m)の公差は±1mmで,これは機器固有の系統誤差となります。 s=0.5mで被測定抵抗を測定した場合,これによる誤差は±0.2%と精度にほとんど影響を与えないことが分ります。
また,ブリッジ回路を構成するリード線は銅線なので抵抗率の差と断面積の違いから,リード線長の影響は無視できることも分ります。
- 参考:0℃での抵抗率
- NiCr:107.3×10-8 Ωm
- Cu:1.55×10-8 Ωm
参考資料
| Rx±ΔRx [Ω] 公称値±公差 |
Rref±ΔRref [Ω] 公称値±公差 |
±Δs [cm] | 算出した Rx±ΔRx [Ω] |
|---|---|---|---|
| 100±1 | 10.00±0.05 | 91.00±0.05 | 101.1±0.8 |
| 100±1 | 50.00±0.25 | 66.80±0.05 | 100.6±0.6 |
| 100±1 | 100.0±0.5 | 50.10±0.05 | 100.4±0.5 |
| 100±1 | 500.0±2.5 | 16.80±0.05 | 101.0±0.6 |
| 100±1 | 1000±5 | 9.15±0.05 | 100.7±0.8 |
| 1000±10 | 100.0±0.5 | 91.00±0.05 | 1011±8 |
| 1000±10 | 500.0±2.5 | 66.75±0.05 | 1004±6 |
| 1000±10 | 1000±5 | 50.05±0.05 | 1002±5 |
| 1000±10 | 5000±25 | 16.75±0.05 | 1006±6 |
| 1000±10 | 10000±50 | 9.15±0.05 | 1007±8 |