ローレンツ力

実験番号:UE3030300
本実験ではローレンツ力を,磁場の中で電流がながれている銅のロッドを吊るすことで測定します。銅のロッドに電流を流すことで力が働き,ある角度で止まります。その傾き(重力とのつり合い点)を測定し,ローレンツ力の大きさを求めます。ローレンツ力の大きさは,電流値,磁場の強さ,銅のロッドの有効長(磁場中に入っている長さ)に影響を受けるので,これら全てを変えて依存性を見ます。また,ローレンツ力の応用として,渦電流による制動力も検証します。
実験の手順
- 電流が流れている導体に働くローレンツ力を,電流・導体の有効長・磁場の強さを変えて測定します。
- 切り込みのある振り子とない振り子で渦電流による制動力の違いを検証します。
実験に必要な機器
- U10371:電磁気実験振り子 ×1
- U10370:磁極間隔可変磁石 ×1
- U13812:プラグ付き安全リード線・75cm・2本セット ×1
- 直流電源,20V,5A ×1 (別途ご用意ください)
実験解説書
基本原理
磁場中の電子は,磁場と電子の運動方向に垂直な向きに力を受けます。この力をローレンツ力と言いますが,電子1個に働く力は小さく直接測るのは困難です。(例えば,比電荷e/m測定実験は電子線という電子の定常的な流れに働くローレンツ力を測定しています。)しかしローレンツ力は導体中の電子にも働くので,磁場中の電流が流れている導体に働く力は,伝導電子に働くローレンツ力の合計となり,測定が容易となります。
直線状で,長さL,断面積Aの導体中の電子数Nは,次のように表せます。
(1)\( N = n_e \cdot A \cdot L \)
ここでneは電子数密度です。各電子が速度vで移動するときに測定される電流値Iは次のようになります。
(2)\( I = n_e \cdot e \cdot A \cdot v \)
この導体が磁束密度Bの磁場中にあると,導体に働く力Fは
(3)\( \vec { F } = n_e \cdot e \cdot A \cdot L \cdot \vec { v } \times \vec { B } \)
(ここでF,v,Bはベクトル,×はベクトル積)であり,vとBのなす角は90°なので絶対値で表せば
(4)\( F = I \cdot L \cdot B \)
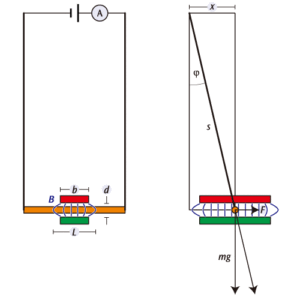
となります。Fの向きは,電流の向きと磁場の向きに垂直になります。この実験では,磁場中に銅のロッドを吊り下げて測定を行います。銅のロッドが力を受けて角度φで重力とつり合い,止まります。この角度φから導体に働く力を計算します。この実験では電流値を変えることや,導体の磁場中の長さ,磁場の強さを変えることで,ローレンツ力のこれらに対する依存性を調べます。銅のロッドが角度\( \varphi \)で静止したとき,導体に働く重力とローレンツ力が釣り合っています。
(図1)この力の大きさは
(5) \( F = m \cdot g \cdot \tan \varphi \)
であり,本実験セットの銅ロッドの質量mは約6.23gです。
磁束密度Bは,磁極間隔可変磁石により与えられています。極間隔を変えることで,磁束密度Bも変わります。また磁極片は回転させることができるので,90°回転させると銅のロッドの有効長(磁場内にある導体の長さ)を変えられます。
測定結果の精度を確保するため,磁場の均一性を検証します。磁極片中央の領域は,磁場は均一で磁極片に垂直に磁束が入ります。しかし磁極片の端部ではこの均一性は成り立たず,磁束は外側に膨らんでいます。この効果を実験に取り込むために,導体の有効長を次のように補正します。
(6)\( L = b + d \)
ここでdは,磁極片間隔です。この式は良い近似で成り立ちます。また,tan\( \varphi \)は実際の振り子の長さと移動距離の測定から計算できます。
渦電流
本実験器に付属の2枚の振り子で比較実験をします。可変磁石の距離を変えないまま2つの振り子を同じ角度から揺らし始めると,切り込みのある振り子は振り子運動を続けますが,切り込みのない振り子は磁石間で急激に減速して止まります。
この現象もローレンツ力によるものです。
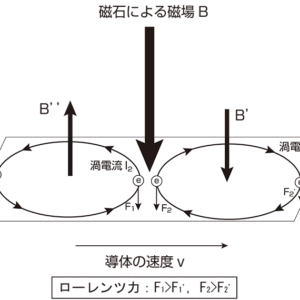
図3のように磁場Bがゼロではない空間を導体が移動するときには,導体中の自由電子が磁場中を運動していることになるので,この電子にはローレンツ力が働きます。
磁石の端では磁束密度が小さくなるため,導体中の電子が受けるローレンツ力は差が生じます。その為,電子が押し出されるように,磁石直下の導体部から円電流(渦電流)が流れます。渦電流は磁場中心に対して左右で逆向きの流れとなり,それぞれの渦電流が作る磁場が制動力となって振り子が止まります。
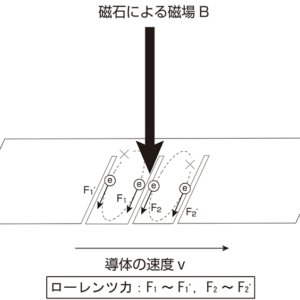
電子が受けるローレンツ力の向きは全て同一なので,磁束密度に差異が無いと電流が発生しません(図4)。これは切り込みがある振り子に相当します。切り込みにより導体幅が小さくなると電子が受けるローレンツ力が両端でほぼ同じとなり,電流がほとんど流れない状態になります。
評価
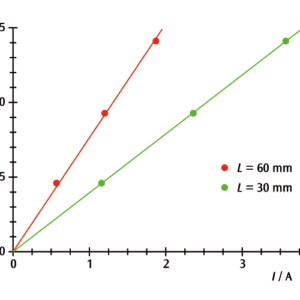
実験結果からローレンツ力の大きさは磁場中の導体長が同じであれば電流値に比例することが分かります(図2)。この時の傾きは式(4)からB・Lとなります。導体長で規格化することで磁束密度Bとなりますが,L=30mmと60mmでこの値はほぼ一致しています。
参考資料
-
図1:磁場中の導体(正面と側面図)
-
図2:導体有効長ごとの電流値とローレンツ力のグラフ
-
図3:磁場中の導体に発生する渦電流
-
図4:切り込みがある場合の導体に働くローレンツ力