ケーターの可逆振り子

実験番号:UE1050221
可逆振り子は,正確な重力加速度を求めるための装置です。可逆振り子には支点が2つあり,そのどちらを使っても振動周期が同一になるように調節できます。その場合の振り子の単振り子相当長は,2つの支点間の距離に等しくなります。これにより重心位置や慣性モーメントを求めることなく,振動周期と可逆振り子の単振り子相当長とを使って 計測地点における重力加速度が求められます。
可逆振り子は,2つの支点の外側にある,より重いおもりの位置を固定したまま,支点間にあるおもりの位置を調整することで,振動周期を一致させます。
実験の手順
- 2つの支点,どちらでも振動周期が同じになるように,可逆振り子を調整します。
- この時の振動周期から,計測地点における重力加速度を計算します。
実験に必要な機器
実験解説書
基本原理
可逆振り子は2つの支点を持つ実体振り子で,取り付けられたおもりを移動させることで2つの支点での振動周期を一致させることができます。この時,単振り子相当長は支点間の距離となり,周期と単振り子相当長から,慣性モーメントや重心位置を求めることなく,計測地点での重力加速度を計算することが可能となります。
実体振り子が静止位置からの角度φで自由に振動する場合,その運動方程式は以下のようになります。
\[ J \cdot \frac {d^2 \phi } { dt^2 } = – m \cdot g \cdot s \cdot sin { \phi } \]
今,角度φが十分小さくsinφ~φと書ける場合,次の形になります。(本実験器では振幅を5cm以下にしてください)
(1) \( \frac { J } { m \cdot s} \cdot \ddot { \phi } + g \cdot \phi = 0 \)
- J: 振動軸に関する慣性モーメント
- g: 重力加速度
- m: 振り子の質量
- s: 振動軸と重心との距離
ここで実体振り子の単振り子相当長Lを求めます。単振り子相当長Lとは「その長さの理想的な単振り子と同じ周期になる」Lという意味です。理想的な単振り子の運動方程式は \(L \cdot \ddot { \phi } + g \cdot \phi = 0 \) なので,式(1)から明らかにLは
(2) \( L = \frac { J } { m \cdot s } \)
となります。
また,平行軸の定理を使うと,振り子の慣性モーメントは以下のように与えられます。
\[ J = J_s + m \cdot s^2 \]
- \( J_s \) :重心を通る軸の周りの慣性モーメント
これを単振り子相当長Lの式(2)と組み合わせると
(3) \( L = \frac { J_s } { m \cdot s } + s \)
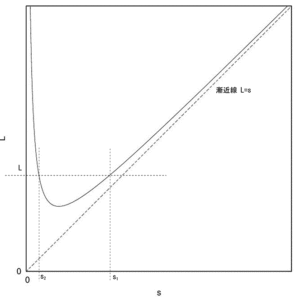
となり,s-L平面上の \(s = \sqrt { \frac { J_s } { m } } \)で極小値を持つ下に凸の曲線になります。(図2)
その為,極小値以外では同じ単振り子相当長となる2つのsが存在します。単振り子相当長が等しいので,周期Tも等しくなります。本実験装置はこの性質を利用しています。
周期Tが等しいときの重心から支点までの距離2つをs1,s2とし,この時の単振り子相当長をLとすると次の式が成り立ちます。
\[ \frac { J_s } { m \cdot s_1 } + s_1 = \frac { J_s } { m \cdot s_2 } +s_2 = L \]
s2について解けば
\[ s_2 = \frac { L } { 2 } \pm \sqrt { \frac { L^2 } { 4 } – \frac { J_s } { m } } \]
s1も同じ式となるのでs1>s2とすると,第二項正がs1,負がs2になります。
一方,本実験装置は距離が d だけ離れた2つの支点を持つ可逆振り子なので,片方の重心までの距離sならば,他方の重心までの距離はd-sとなります。sとd-sのどちらか大きい方は上式s1,短い方をs2と代入することで,次の結果を得ます。
(4)\( L = d \)
\[ s_1 = \frac { d } { 2 } + \sqrt{ \frac { d^2 } { 4 } – \frac { J_s } { m } } ),( s_2 = \frac { d } { 2 } – \sqrt{ \frac { d^2 } { 4 } – \frac { J_s } { m } } ),( T = 2 \pi \cdot \sqrt { \frac { d } { g } } \]
可逆振り子で両支点での周期が等しくなるように調節すると,単振り子相当長は支点間距離dに等しくなること,その時の周期Tは振り子の実際の慣性モーメントや重心位置に依存しないことが分かります。
本実験では,2つの支点の間にある質量 m2 = 1 kg のおもりを適宜動かすことにより,可逆振り子の振動周期を一致させることができます。もう一方のおもり,質量 m1 = 1.4 kg は,2つの支点の外側に固定されています。周期は,振り子の下端が振動の中心位置を通過する時間をストップウォッチで計測することで求めます。(振動体の周期測定方法を参照)
これにより,単振り子相当長 L1 と L2 とに対する振動周期 T1 と T2 を,質量 m2 のおもりの位置 x2 の関数としてグラフをプロットします。
評価
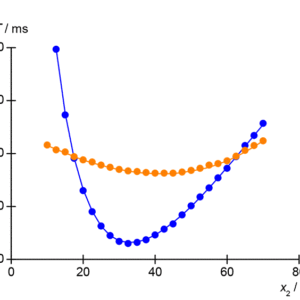
2つの振動周期 T1(x2) と T2(x2) の曲線は,周期が T = T1 = T2 を満たす点で2度交わります。交点の正確な位置(x2の値)を決めるには,測定点の内挿が必要になります。重力加速度は,本実験装置の加工精度から0.03% の相対精度で,以下のように計算できます。
(5) \( g = \left( \frac {2\pi} {T} \right) ^2 \cdot d \, \, , \, \, d=0.8m \)
ここでdは,支点間距離です。
参考資料
-
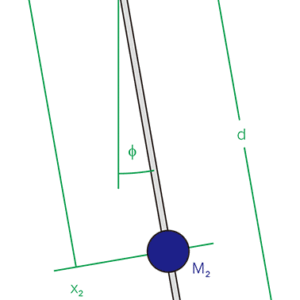
図1:可逆振り子の概念図
-
図2:支点-重心間距離sと単振り子相当長Lのグラフ)
-
図3:質量 m2 のおもり位置 x2 に対する周期 T1 と T2 の測定値)