マイケルソン干渉計

実験番号：UE4030410

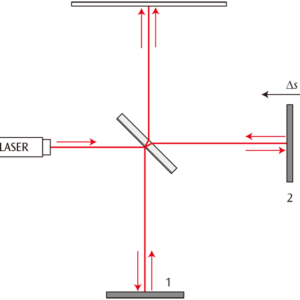
マイケルソン干渉計では光路にハーフミラーを置くことで，光をそれぞれ別の方向へ進む2 本の光に分割します。分かれた光はそれぞれ光路の端で鏡により反射され，もとの光路を戻り再び結合されます。この時に2本の光路にわずかでも差があると，スクリーンの干渉縞が変化するため分かります。

実験の手順

レーザー光の波長を測定します。
ガラスの屈折率を測定します。
空気の屈折率の圧力依存性を測定します。

実験に必要な機器

お見積りフォーム

実験解説書

実験解説書ダウンロード（PDF）

基本原理

マイケルソン干渉計は，かつて光の媒質として考えられていたエーテルに対する地球の運動を検出するために，マイケルソンによって発明されました。この干渉計は光路の微小な差異を感度良く検出します。

装置に入射した光がハーフミラーで2つに分割され別の光路を通り，それぞれの終端におかれた鏡で反射され再度ハーフミラーで結合されます。この為，スクリーンに干渉縞が現れます。（図1）干渉縞は光路の差異に敏感に反応するので，干渉計を構成している部品の熱膨張さえも検出します。

i），レーザー光源波長測定

片側の光路が長くなったり短くなったりすると干渉縞の数が増えたり減ったりします。光路の変化長Δsと暗線干渉条件は光の波長λを使い次のようになります。

(1)\(2 \Delta s = m \lambda\)

ここでmは増減した干渉縞の数を表す正負の整数です。この関係を用い，可動鏡（写真右側）を微小距離Δxだけ移動させて光の波長を測定します。微小な移動距離Δxは可動鏡に接続されたマイクロメーターネジにより正確に読み取れます。またこの時は空気の屈折率をn=1としても十分です。

それゆえ（1）式のΔsはΔxと等しく，波長λは実験結果から次のように計算されます。

(2)\(\lambda = \frac {2 \Delta x}{m}\)

ii），ガラスの屈折率測定

（計算詳細等は「ガラスの屈折率の計算」(PDF)を参照）

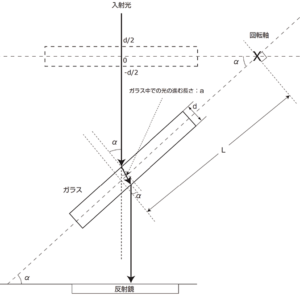
この実験では屈折率を測定する光学ガラス板を光線に対し垂直に入れた状態からガラス板を傾けていき，その時の波数の変化から屈折率を求めます。そのため，初期状態（ガラス板が光線に対し垂直な状態）からの光路の変化は，最初にハーフミラーで反射され分割された光の光路差を考えるだけで十分です。

ミラーを回転させることで変化する光路差を考えるために，ガラス中の光路差を ⊿S1 ，空気中の光路差を ⊿S2 とします。

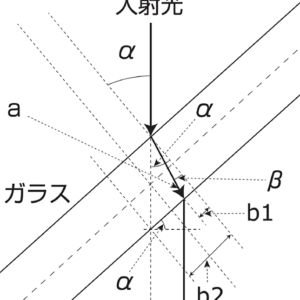
(3) \[ \Delta S_1 = a-d = d\left(c\frac{1}{\cos{\beta}}-1\right) \]

(4) \[ \begin{align} \Delta S_2 &= d \left\{ \left( 1 – \frac{1}{\cos {\alpha}} \right) + (\tan{\alpha} – \tan{\beta}) \sin{\alpha} \right\} \end{align} \]

光はミラーにより反射するため，同じ経路を2回通ります。よって，この変化による波数の差⊿k は次のとおりです。

(5) \[ \Delta k = \frac{2}{\lambda} \left(n_G \Delta S_1 + \Delta S_2 \right) \label{eq:dk} \]

⊿k が整数のとき，リングの中心で ( 明→ ) 暗→明 ( →暗 ) の繰り返しが整数回となるので，その値をmとすれば

(6) \[ m = \frac{2}{\lambda} \left(n_G \Delta S_1 + \Delta S_2 \right) \]

となります。

nGについて整理すれば，nGの三次方程式になり，解の公式に測定で得られる係数を代入して具体的な屈折率を計算します。ミラーの角度が小さいときには初期角度φ0の影響が大きく，少しの読み取り誤差で影響が出るので，m>30で屈折率を求めます。実験ではnG=1.63となりました。

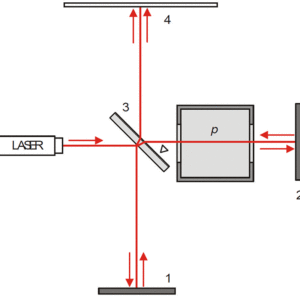
iii），空気の屈折率の圧力依存性

（計算詳細は「空気の屈折率測定」(PDF)を参照）

空気の屈折率は近似的に圧力に比例します。そのため空気の屈折率を次の式で求めます。

(7) \[n(p)=1 + \frac{\Delta n}{\Delta p} \Delta p\]

屈折率の変化を干渉計で測定可能な光路差に置き換えれば，屈折率の圧力依存係数は次の形となります。

(8) \[ \frac{\Delta n}{\Delta p} = \frac{\lambda_0}{2I_z} \frac{\Delta m}{\Delta p} \]

ここでIzはキュベットの光軸方向の内寸で，λ0は光源の真空中の波長， ⊿mは干渉縞数の変化となります。

このように干渉縞の変化数と圧力の変化から，屈折率の圧力依存係数を求めることができます。

評価

i），レーザー光源波長

実測では初期状態（m=0）とm=+30でそれぞれマイクロメーターの読みが19.98mm，10.10mmでした。マイクロメーターの読みと可動鏡の実際の移動距離は1mm:970nm（メーカー値）なので，これより光源波長λは次のように計算できます。

(9) \[ 2 \frac{\Delta x}{m}=\frac{2 \times (19.98-10.10) \times 970}{30}=639 \, \mathrm{nm} \]

使用光源はHe-Neレーザーでλ=633nmなので測定結果は約 1%大きくなっています。

ii)，ガラスの屈折率

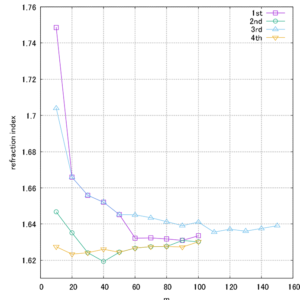
ガラスの屈折率を測定する時は最初に光路に入れるガラスとハーフミラーが正確に45°をなしていることが必要です。この精度を機器加工で出すことは難しいため，45°となるようにガラスの初期角度を微調整します。以降，測定するガラスの角度と干渉縞変化数は，この初期角度の補正をした後に屈折率を計算します。測定結果は図5のようにnGは約1.63～1.64でした。

iii），空気の屈折率の圧力依存性

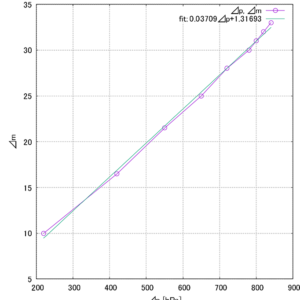
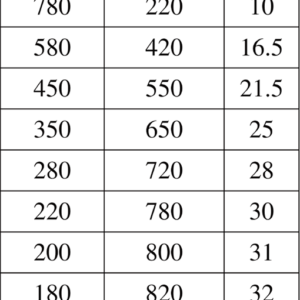
キュベットを大気圧から徐々に減圧し，干渉縞数の変化を測定しました。大気圧 p 0 = 1000[hPa] を取りました。また， Δp = |p 0 － p| ， p: キュベット内圧力 [hPa] です。表 1 が測定結果です。同様に⊿mも絶対値を取っています。また，測定結果と最小二乗法でフィッティングした近似直線を図6 に示しました。

図6 から Δm/Δp = 0.037 で，キュベットの光線方向の内寸は 41mm です。よって Δn/Δp は(8) 式より次のようになります。

\[ \frac{\Delta n}{\Delta p} = \frac{\lambda_0}{2I_z}\times 0.037 \]\[ = 0.29\times {10}^{-6} \, \mathrm{\frac{1}{hPa}} \]

理科年表ではT = 15℃, p = 1013.25 hPa の乾燥空気で n ～1.000277 となっているので， (7) 式に p = 1013.25 hPa を代入した値 1.000294 が良く空気の屈折率を表していることが分かります。