連成振動

実験番号:UE1050600
2つの等価な棒振り子をバネで接続した連成振動は,振り子がある周期で振動するとともに振幅のうなり(振幅が減少と増加を繰り返す)が見られます。 この周期とうなりの周期は2つの振り子が同位相と逆位相の場合の振動の重ね合わせで記述できます。
実験の手順
- 2つの振り子が同位相の場合の周期\( T_+ \)を測定します。
- 2つの振り子が逆位相の場合の周期\( T_- \)を測定します。
- 任意の初期状態での2つの振り子の連成振動で,周期Tと振幅のうなりの周期\( T_{Δ}\)を測定します。
- \( T_{Δ}\),\( T_+ \)と\( T_- \)を運動方程式の結果を用いて比較します
実験に必要な機器
- U8404275-115:角度センサー付き棒振り子 ×2
- U15027:つる巻きばね・3.9N/m ×1
- U13260:支柱用テーブルクランプ ×2
- U15004:ステンレス鋼製支柱・100cm ×2
- U15002:ステンレス鋼製支柱・47cm ×1
- U13255:角型ムッフ ×4
- U11259:BNC-4mmジャック変換アダプター ×2
- 1022284:WiLab ×1
- UCMA-BT32I:差動型電圧センサー 500 mV ×2
- UCMA-BTSC1:センサー接続ケーブル ×2
- Windows PC ×1(別途ご用意ください)
- Coach 7はデータ収集・解析用 PC ソフトウェアです。有効期限付きとなり,使用者数規模・有効期限長によりライセンス料金が変わります。詳しくは弊社までお問い合わせください
実験解説書
参考 連成振動の運動方程式(含ラグランジュの方程式) ダウンロード(PDF)
基本原理
2つの振り子をバネで接続した連成振動では,エネルギーが2つの振り子を行き来する様子が観察できます。より分かりやすく観察する例として,2つの等価な振り子をバネで接続します。1つは振り子の最下点で静止し,もう1つは任意の角度から静かに手を離します。この場合はエネルギーの完全な往復が起こり,一方の振り子が最大振幅となるときに他方は最下点でほぼ静止した状態を互いに繰り返します。
2つの等価な振り子のをバネで接続した連成振動は,2つの規準振動の重ね合わせで表せます。この系での規準振動は2つの振り子が同位相と逆位相の2つです。同位相は,2つの振り子は同じ角振動数で位相差が0の場合です。このとき2つの振り子を接続するバネは伸縮を行わず,そのため各振り子は独立に振動している状態です。逆位相は,2つの振り子は同じ各振動数ですが位相がπずれている状態です。これはバネの影響が一番大きな条件となります。
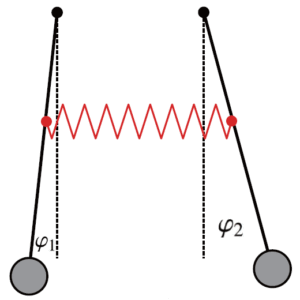
これを運動方程式で見てみます。力学的モデル及び\( \varphi_1,\,\varphi_2 \)については図1を参照してください。
(1) \[ L\ddot{\varphi}_1+g\varphi_1+c(\varphi_1-\varphi_2) =0 \]\[ L\ddot{\varphi}_2+g\varphi_2+c(\varphi_2-\varphi_1) =0 \]
ここで
L:振り子の長さ
g:重力加速度
c:2つの振り子の結合定数(バネ定数を含みますが,それ以外のバネ取り付け位置等のパラメータも含めたものです)
です。
2つの式が対称なので,次の変数変換をします。
(2)\[ \varphi_+ =\displaystyle \frac{\varphi_1+\varphi_2}{2} \]\[ \varphi_- =\displaystyle \frac{\varphi_1-\varphi_2}{2} \]
よって運動方程式(1)は次のように,分離された2つの微分方程式に帰着します。
(3)\[ L\ddot{\varphi}_++g\varphi_+ =0 \]\[ L\ddot{\varphi}_-+(g+2c)\varphi_- =0 \]
2つとも単振動の式であり,解は次のようになります。
(4)\[ \varphi_+= Asin{(\omega_+ t + \varphi_+)} \]\[ \varphi_-= Bsin{(\omega_- t + \varphi_-)} \]
ここで
(5)\[ \omega_+ = \sqrt{\displaystyle \frac{g}{L}} \]\[ \omega_- = \sqrt{\displaystyle \frac{g+2c}{L}} \]
であり,\( A,B,\varphi_+,\varphi_- \) は初期条件で決まるそれぞれの振幅と初期位相です。\( \varphi_1,\varphi_2 \) に書き直せば次のとおりです。
(6)\[ \varphi_1 = \frac {1}{2} { Asin{(\omega_+ t + \varphi_+)} + Bsin{(\omega_- t +\varphi_-)} } \]\[ \varphi_2 = \frac {1}{2} { Asin{(\omega_+ t + \varphi_+)} – Bsin{(\omega_- t +\varphi_-)} } \]
式が入り組んでいるので,分かりやすい例として次のような初期条件を考えます。
(7)\[ \varphi_1 = \varphi_0 \quad \, , \, \quad \dot{\varphi}_1 = 0 \]\[ \varphi_2 = 0 \quad \, , \, \quad \dot{\varphi}_2 = 0 \]
実験としては,右側の振り子を軽く手で抑えておき,左側の振り子を適当な角度に保持して,同時に手を離す,というものです。計算詳細は別紙に譲りますが,\( \varphi_1 , \varphi_2 \)は次のように表されます。
(8)\[ \varphi_1=\varphi_0cos{(\omega_{\Delta}t)}cos{(\omega t)} \]\[ \varphi_2=\varphi_0sin{(\omega_{\Delta}t)}sin{(\omega t)} \]
ここで
(9)\[ \omega=\frac{\omega_+ +\omega_-}{2} \]\[ \omega_{\Delta}=\frac{\omega_- -\omega_+}{2} \]
(8)式を見ると,2つの振り子は位相が \( \pi /2 \) ずれた振動(角振動数 \( \omega \))で,振幅が周期 \( T_{\Delta}=\pi/\omega_{\Delta} \) の長い周期で0から \( \varphi_0 \) の移り変わりを続けるということが分かります。(\( \omega > \omega_{\Delta} \))
通常,うなりの周期として振幅が最小から最小になる時間間隔を取ります。しかし,式からも分かる通り\( sin{(\omega_{\Delta}t)} \)の1周期は振幅が\( 0\rightarrow + \rightarrow 0 \rightarrow – \rightarrow 0 \)なので,測定するうなりの周期の2倍になります。
実験で測定する同位相の周期を \( T_+ \),逆位相の周期を\( T_- \)とすれば,一般の連成振動の周期Tと振幅のうなり周期\( T_{Δ}\)の関係は次のようになります。
(10) \[ \omega_+=\frac{2\pi}{T_+} , \,\omega_-=\frac{2\pi}{T_-} \]
よって(8)(9)式より
(11) \[ T=\frac{2\pi}{\omega} =\frac{4\pi}{\omega_++\omega_-} =2\frac{T_+T_-}{T_++T_-} \]
同様に
(12) \[ T_{\Delta}=\frac{\pi}{\omega_{\Delta}}=\frac{T_+T_-}{T_+-T_-} \]
となります。
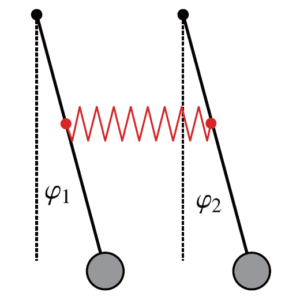
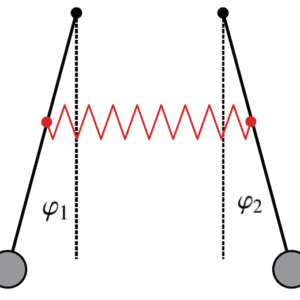
図1:2つの振り子の一般の連成振動と同位相・逆位相の場合
-
( varphi_1 = varphi_2 ) 一般の連成振動
-
( varphi_1 neq varphi_2 ) 同位相
-
( -varphi_1 = varphi_2 ) 逆位相
実験の手順
- 同位相の周期を測定します。同一の小さな角度で2つの振り子を同じ側へ動かし,同時に手を離します。時間tと振り子の角度の時間グラフを取り,周期を測定します。
- 逆位相の周期を測定します。同一の小さな角度で2つの振り子を反対側へ動かし,同時に手を離します。時間tと振り子の角度の時間グラフを取り周期を測定します。
- 上で検討した初期条件での時間tと振り子の角度のグラフを取ります。このとき振り子の短い周期とうなりの長い周期を測定します。
- 同位相・逆位相の規準振動周期と振り子周期・うなり周期が,上で検討した関係を満たすか確認します。
- その他,任意の初期条件で振り子周期とうなり周期を測定し,規準振動周期と比較します。
測定例:(L=75cm,バネ取り付け位置=40cm,バネ定数k=3N/m)
-
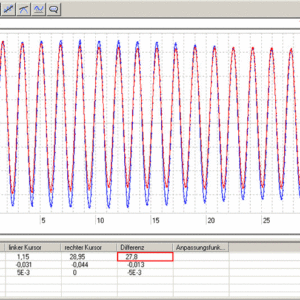
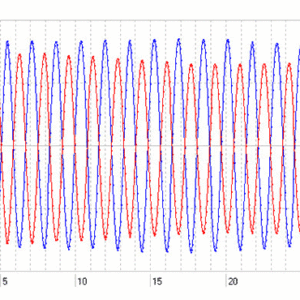
図2:同位相での振幅波形(赤枠内:カーソル間の時間 27.8s)
-
図3:逆位相での振幅波形
-
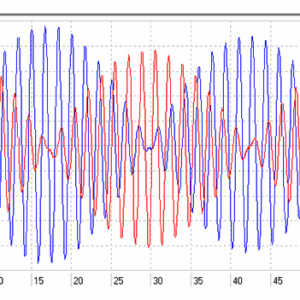
図4:検討した初期条件での振幅波形(カーソル間:うなりの周期)
-
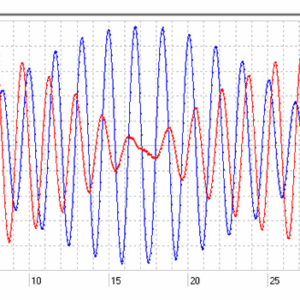
図5:図4の拡大図(カーソル間:角振動数 の16周期分)
検討:
図2より同位相では16周期で27.8sなので,
\[ T_+=\frac{27.8}{16}=1.738 \mathrm{s} \]
同様に
\[ T_-=1.629 s \]\[ T=1.685 s \]\[ T_{\Delta}=25 s \]
これより
\[ 2\frac{T_+T_-}{T_++T_-}= 1.682 \mathrm{s} \] \[ \frac{T_+T_-}{T_+-T_-}= 25.97 \mathrm{s} \]
と計算できます。
周期Tは運動方程式から導いた関係である(11)式と良い一致を見せています。一方,\( T_{\Delta} \)は約1秒のズレがあります。(12) 式は\( T_+ \)と\( T_- \)の差が分母にあり,それぞれの誤差が数msでも大きな違いを生じてしまいます。合わせこむとすれば,分母を約4ms大きくすることで,ほぼ実測値と一致します。
次に測定データから2つの振り子の結合定数cを求めてみます。ここでの結合定数cは重力加速度gより非常に小さく,周期\( T_- \)に対する影響は小さくなっています。しかし,結合定数cの影響はうなりの周期では支配的であるため,\( T_- \)から直接求める求めるのではなく,うなりの周期\( T_{\Delta} \)を使うことを考えます。
(5)(9)式より次の関係を得ます。
(13) \[ c=2L(\omega_{\Delta}^2+\omega_+\omega_{\Delta}) \]
角振動数を周期に書き換えれば
(14) \[ c=2\pi^2L\left(\displaystyle \frac{1}{T_{\Delta}^2}+\displaystyle \frac{2}{T_+T_{\Delta}}\right) \]
であり,L=0.75mとそれぞれの周期からC=0.71と見積もれます。(次元は加速度と同じになります。)
別紙計算より,2つの振り子の結合定数cとバネ定数kは次の式で結ばれます。
(15) \[ c=\frac{kL’^2}{mL} \]
ここで k はバネ定数,L’は支点からバネ取り付け位置までの距離,mは振り子1つの質量です。この式でバネ定数を計算すると \( k=3.31\mathrm{N/m}\)と約10%大きくなっています。